Matemáticas
para estudiantes de 8.o grado
En 8.° grado, los estudiantes se enfocan en la resolución de problemas con funciones y ecuaciones lineales.
Los estudiantes deben trabajar juntos en clase, hablar sobre cómo resuelven los problemas y aprender unos de otros. Deben usar la tecnología para ver y graficar ecuaciones y datos. Los estudiantes de 8.º grado deben formular argumentos matemáticos y probar distintas formas de resolver problemas. Deberán resolver problemas numéricos y textuales, incluidos problemas del mundo real. Por último, deben estimar las soluciones antes de resolver y saber si su estimación es razonable. Los estudiantes de 8.° grado pasarán la mayor parte del tiempo aprendiendo los siguientes temas. Deben saberlos bien antes de fin de año.
Tip (NEEDS TRANSLATING): Hover over icons to see definitions of key terms.
This is an example tooltip! (NEEDS TRANSLATING)

LO QUE SU HIJO DEBE SABER Y DEBE PODER HACER
APRENDER MATEMÁTICA DE 8.° GRADO
Describir el valor de los números que no son racionales usando números racionales.
√ 7 es no racional porque no puede representarse mediante una fracción. El valor de √ 7 se encuentra entre 2.6 y 2.7.

Resolver problemas con exponentes complejos, incluidos exponentes que son números negativos y fracciones.
Aplicar propiedades de los exponentes enteros para generar expresiones equivalentes. Usar raíz cuadrada para mostrar la solución de las ecuaciones.
27⅔ = ∛272 = ∛729 = 9
Escribir número grandes y pequeños usando notacióncientífica; multiplicar y dividir con número en notación científica.
86,000 → 8.6 x 104
4.2 x 10-4 → 0.00042
Resolver problemas con ecuaciones lineales en una variable y sistemas de ecuaciones lineales. Representar y graficar relaciones de problemas matemáticos y de la vida real usando ecuaciones lineales.
Utilizar ecuaciones lineales para mostrar situaciones proporcionales. Encontrar la pendiente y la intersección cony.
y=mx+b
- y and x are variables
- m is the slope of the line
- b is the y-intercept, or where the line crosses the y-axis
Estudiar detenidamente los patrones y las relaciones en los datos que involucran dos variables. Utilizar funciones para modelar relaciones entre dos variables. Crear e interpretar funciones lineales con tablas, gráficos y ecuaciones.
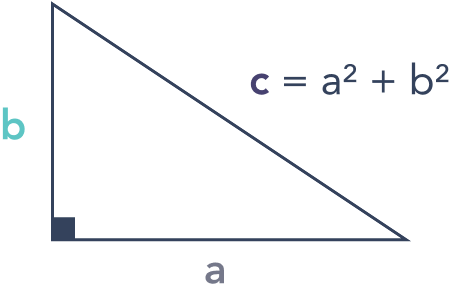
Justificar y usar el Teorema de Pitágoras para resolver problemas.
Para un triángulo rectángulo (un triángulo con un ángulo) a2 + b2 = c2
EJEMPLOS DE MATEMÁTICAS PARA 8.°
¿Cuáles de las siguientes son expresiones irracionales?
- 4√18
- √16 + √25
- 12√4
- 4 + √16
- 10√9
- 3 + √15
4√18, 3 + √15
En la recta numérica se muestran cuatro puntos, ¿qué punto representa√9?

E
Simplifica cada una de las siguientes expresiones:

20y10, 4/3x3, x15, 3
La superficie terrestre total de China es de aproximadamente 9,326 × 106 kilómetros cuadrados. Escribe la superficie terrestre de China en formato estándar.
9,326,000 kilómetros cuadrados.
Una partícula de polvo pesa 0,000000000753 kilogramos.
¿Cómo se escribe este número en notación científica?
7.53 x 10-10 kilogramos
¿Cuál representa una función no lineal?
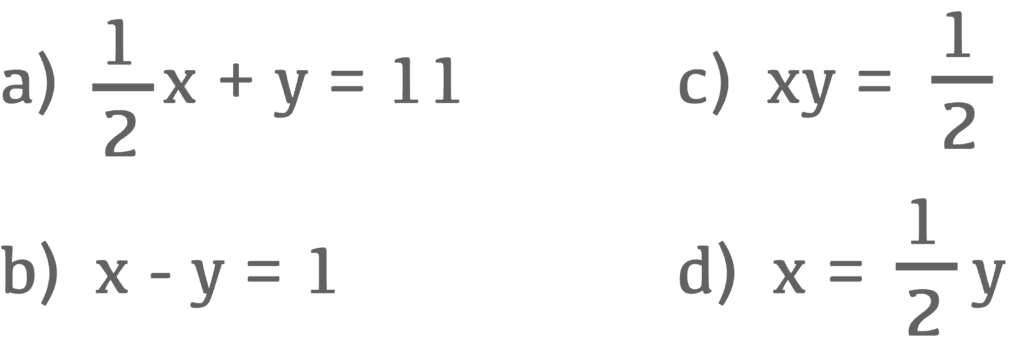
c: xy = 1/2
El costo total de un pedido de libros, c, depende de la cantidad total de libros incluidos en el pedido, b. Escribe una ecuación para mostrar el costo como una función de la cantidad de libros.
c=f(b)
A continuación, se muestra el gráfico de una recta. ¿Cuál es la pendiente de la recta?
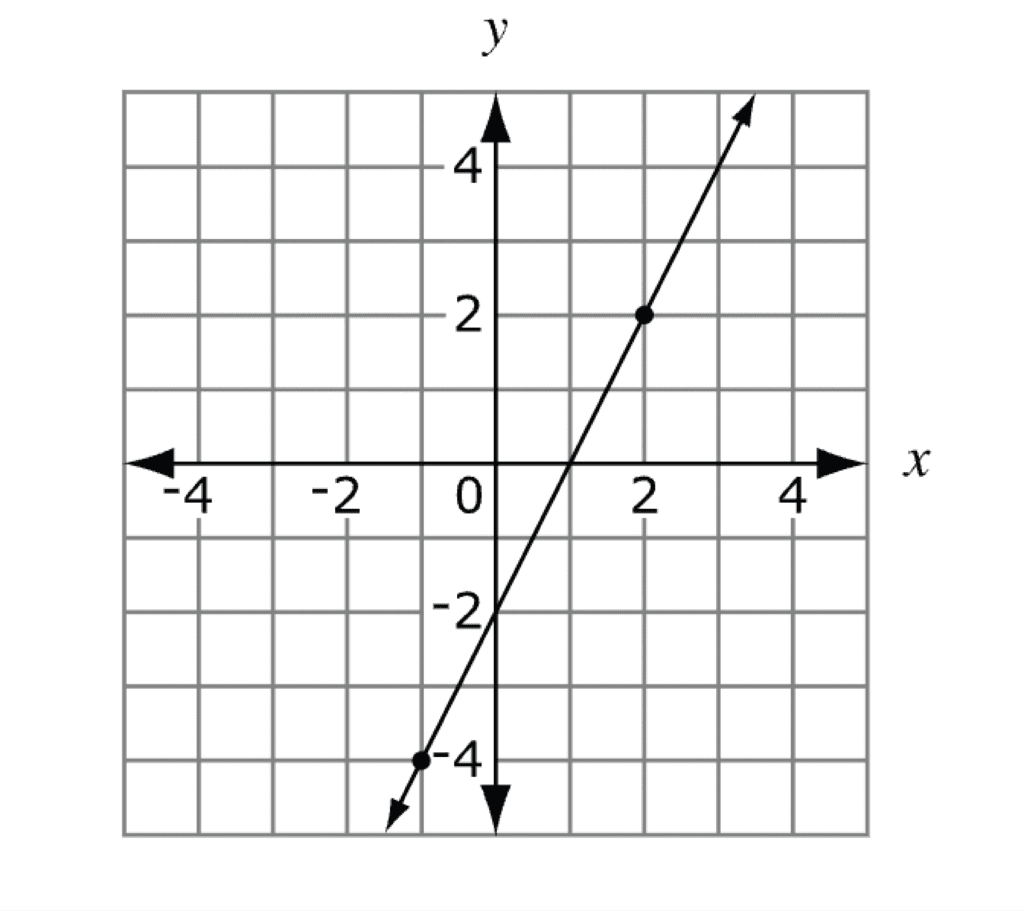
2
Grafica la recta que pasa a través del punto (1, 2) y tiene una pendiente de (-¾)
Deben dibujar una línea que conecte el número 6 en el eje y (eje vertical) y el 7 en el eje x (eje horizontal).
¿Cuál es el valor de 4j−|j−6|cuandoj=−3?
-21
La banda de la escuela está vendiendo barras de dulce para recolectar dinero para un viaje que costará $1.625. Por cada barra de dulce que venden, ganan $0,75. Ya han recolectado $967. Escribe una ecuación que pueda utilizarse para averiguar la cantidad mínima de barras de dulce, n, que deben vender para recolectar el resto del dinero que necesitan para el viaje.
.75n = $658
Los puntos Q(2, 2), R(4, 4) y S(8, 4) son vértices del paralelogramo QRST. ¿Cuál es la ecuación de la recta que incluye ST?
y = x – 4
Grafica la solución para la desigualdad−4x+3>21en la recta numérica a continuación.

x es menor o igual a -4
Example Tooltip
ACTIVIDADES DIARIAS PARA REFORZAR EL APRENDIZAJE
Tips for Talking to Teachers
A strong relationship between families and teachers is key to ensuring students have what they need to succeed. Parent involvement not only leads to higher grades and test scores, but also helps students develop self-confidence, motivation, and social skills. Knowing what questions to ask at school visits and parent-teacher conferences can help you feel confident when it comes to addressing your child’s’ academic needs.

