Mathematics
for 8th Grade Students
See what skills your child will learn in Mathematics, examples of student work and how you can help at home.
Tip: Hover over icons to see definitions of key terms.
This is an example tooltip!

Expectations for Students
By the end of the year, 8th graders need to know:
Learning 8th Grade Mathematics
Describe the value of numbers that are not rational by using rational numbers
√7 is not rational because it cannot be represented by a fraction. The value of √7 is between 2.6 and 2.7.

Solve problems with complicated exponents including exponents that are negative numbers & fractions
Apply properties of integer exponents to generate equivalent expressions. Use square roots to show solutions to equations:
27⅔ = ∛272 = ∛729 = 9
Write large & small numbers using scientific notation; multiply & divide with numbers in scientific notation:
86,000 → 8.6 x 104
4.2 x 10-4 → 0.00042
Solve problems with linear equations in one variable & systems of linear equations. Represent & graph relationships from real-world & math problems using linear equations
Use linear equations to show proportional situations. Find the slope & y-intercept:
y=mx+b
- y and x are variables
- m is the slope of the line
- b is the y-intercept, or where the line crosses the y-axis
Look closely at patterns & relationships in data involving two variables. Use functions to model relationships between two variables. Create & interpret linear functions with tables, graphs, & equations
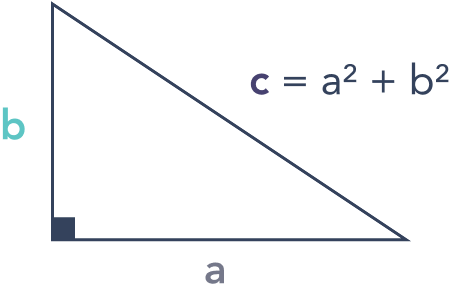
Justify & use the Pythagorean Theorem to solve problems
For a right triangle, (a triangle with a 90° angle) a2 + b2 = c2
Example Student Work
Which of the following are irrational expressions?
- 4√18
- √16 + √25
- 12√4
- 4 + √16
- 10√9
- 3 + √15
4√18 and 3 + √15
Four points are shown on the number line, which point represents √9?
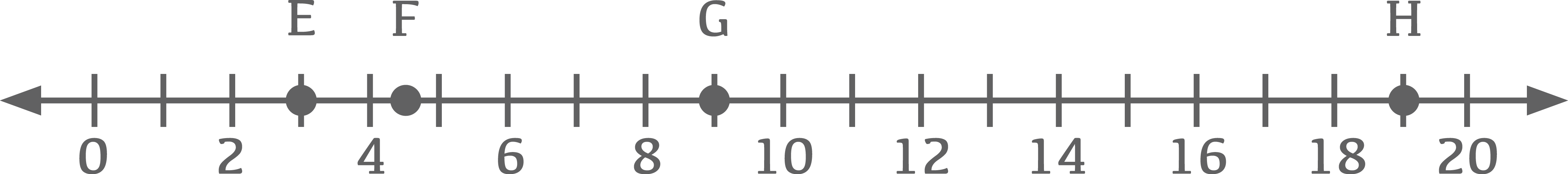
E
Simplify each of the following expressions:
- 10y8 * 2y2=
- 4x3/3x6=
- x20 / x5=
- 2x2 * 3x3 / 2x5=
20y10, 4/3x3, x15, 3
The total land area of China is approximately 9.326 × 106 square kilometers. Write the land area of China in standard form.
9,326,000 square kilometers
A dust particle weighs 0.000000000753 kilograms. What is this number written in scientific notation?
7.53 × 1010kilograms
Which represents a nonlinear function?
- 1/2x+y=11
- x-y=1
- xy=1/2
- x=1/2y
xy=1/2
The total cost of a book order, c, is dependent upon the number of books in the order, b. Write an equation to show the cost as a function of the number of books.
c = f(b)
The graph of a line is shown below. What is the slope of the line?
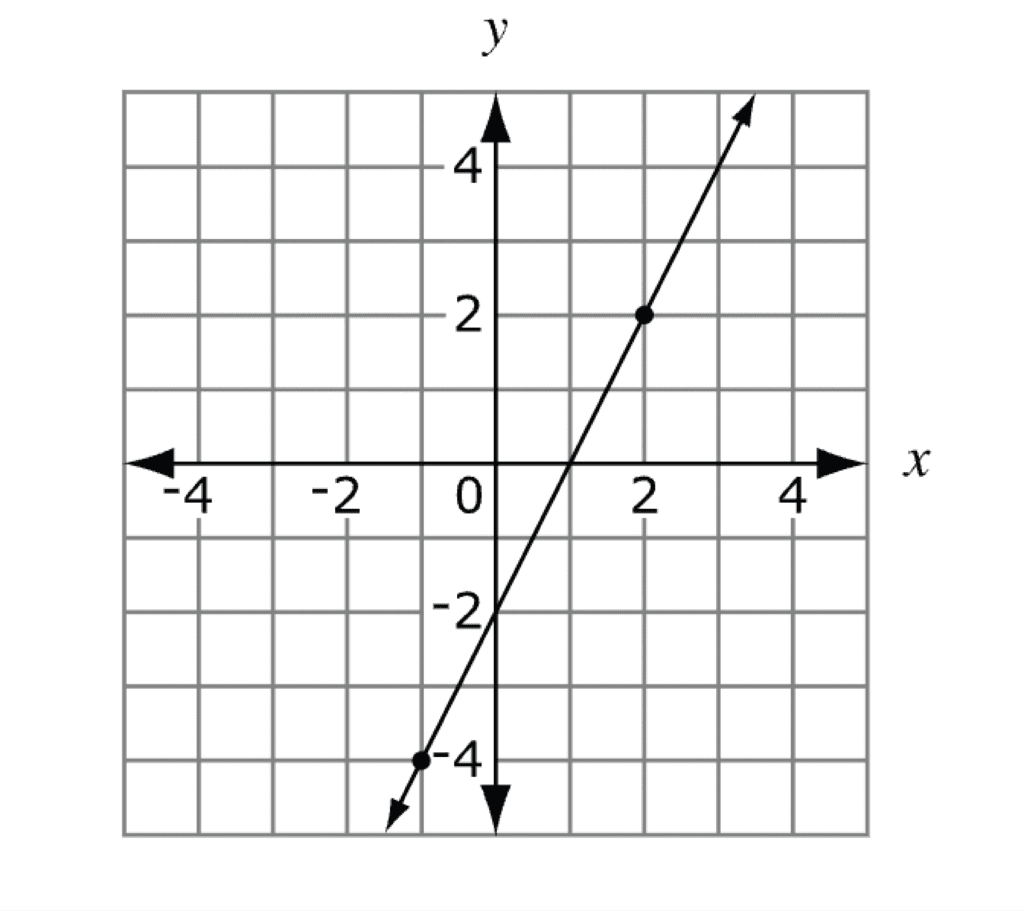
2
Graph the line that passes through the point (1,2) & has a slope of (-3/4).
They should draw a line connecting the number 6 on the y axis (vertical axis) and 7 on the x axis (horizontal axis).
What is the value of 4 j−|j−6|when j=−3?
-21
The school band is selling candy bars to earn money for a trip that will cost $1,625. For each candy bar they sell, they earn $0.75. They have already earned $967. Write an equation that can be used to find the minimum number of candy bars, n, that they must sell to earn the rest of the money for the trip.
0.75n = $658
Points Q(2, 2), R(4, 4), and S(8, 4) are vertices of parallelogram QRST. What is the equation of the line that includes ST?
y = x – 4
Graph the solution to the inequality −4 x+3>21 on the number line below.

x is less than or equal to -4
Example Tooltip
Everyday Activities
Tips for Talking to Teachers
A strong relationship between families and teachers is key to ensuring students have what they need to succeed. Parent involvement not only leads to higher grades and test scores, but also helps students develop self-confidence, motivation, and social skills. Knowing what questions to ask at school visits and parent-teacher conferences can help you feel confident when it comes to addressing your child’s’ academic needs.

